Introduction

This package provides a solver for a system of linear equations. It is an implementation of the tridiagonal matrix algorithm, also known as Thomas algorithm.

System, by example of n = 4 unknowns x:

b[0] * x[0] + c[0] * x[1]                             = d[0]
a[0] * x[0] + b[1] * x[1] + c[1] * x[2]               = d[1]
              a[1] * x[1] + b[2] * x[2] + c[2] * x[3] = d[2]
                            a[2] * x[2] + b[3] * x[3] = d[3]

In matrix notation:

The algorithm is only guaranteed to find a solution if the tridiagonal matrix is diagonally dominant:

|b[0]|   > |c[0]|
|b[1]|   > |a[0]| + |c[1]|
|b[2]|   > |a[1]| + |c[2]|
…
|b[n-1]| > |a[n-2]|

In other words: If that condition is not met, then it may happen that the algorithm cannot find a solution even if one exists.

In case no solution is found, the result is null. For bad input, the result is undefined.

Examples

• Three unknowns:

  

  Input:

  var solve = require('tridiagonal-solve');
  return solve([4, 3], [9, -7, 8], [1, 2], [5, 6, 2]);
  

  Result: [0.6, -0.4, 0.4]

• Matrix is not diagonally dominant, and algorithm fails although solution exists:

  

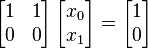
  Snippet: solve([0], [1, 0], [1], [1, 0])

  Result: null

• Solution found although matrix is not diagonally dominant:

  

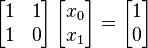
  Snippet: solve([1], [1, 0], [1], [1, 0])

  Result: [0, 1]

Coding conventions

• Code needs to validate with JSLint.

• Comments are in Markdown.

• Avoid constructors (JS is classless), don’t throw exceptions (not necessary in JS).

• Versioning: major.minor.bug-fix

  Incompatible changes to the API mandate an update of the major version.

  Keep version up to date in:

  • Git tags

  • package.json

License

Except where noted otherwise, files are licensed under the MIT License.

The MIT License (MIT)

Copyright (c) 2014 Felix E. Klee

Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.